Electric VLSI Design System User's Manual

Chapter 5: Arcs

5-2: Constraints
5-2-2: Slidable Arcs

Another constraint, available only for nonrigid arcs, is slidability. When an arc is slidable, it may move about within its port. To understand this fully, you should know exactly where the arc endpoint is located. Most arcs are defined to extend past the endpoint by one-half of their width. This means that the arc endpoint is centered in the end of the arc rectangle. If the arc is 2 wide, then the endpoint is indented 1 from the edge of its rectangle. All arc endpoints must be inside of the port to which they connect. If the port is a single point, then there is no question of where the arc may attach. If, however, the port has a larger area, as in the case of contacts, then the arc can actually connect in any number of locations.

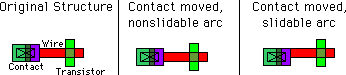
Slidable arcs may adjust themselves within the port area rather than move. For example, if a node's motion is such that the arc can slide without moving, then no change occurs to the arc or to the other node. Without the slidable constraint, the arc moves to stay connected at the same location within the port. Slidability propagation works both ways, because if an arc moves but can slide within the other node's port, then that node does not move. Note that slidability occurs only for complete motions and not for parts of a motion. If the node moves by 10 and can slide by 1, then it pushes the arc by the full 10 and no sliding occurs. In this case, only motions of 1 or less will slide.

Because ports have area, and because arcs end somewhere inside of that area, the actual ending point can vary considerably. If the arc is at the far side of the port, it may protrude out of the far side of the node, causing unwanted extra geometry. You can shorten an arc so that its endpoint is at the closest side of the port with the Shorten Selected Arcs command (in menu Edit / Cleanup Cell).

Table of Contents